Topology is a fundamental discipline, like Algebra and Geometry. Developed in moderntimes, topology is a branch of mathematics that studies the phenomenon of continuity, mainly focusing on invariant properties and topological invariant of a topological space under transformation. Various knots, links and Mobius strip are typical topological structures. Recent studies have shown that topology and physical properties of materials are increasingly linked and the concepts in topology are being applied in many disciplines. In materials science, as well, topology has made contribution to more and more research, especially topological phase factor of quantum mechanical wave function is closely related with many famous physical phenomena. For example, Aharonov-Bohm effect, Berry phase effect, Josephson effect, Quantum Hall effect, de Haas-van Alphen effect and so on, are closely related to topology. Therefore, topology has been developed as the link amongmany disciplines and promotes interdisciplinary scienceand the development of various disciplines. In-depth study of the relationship between the topological structure of metal magnetic materials and magnetic, electromagnetic properties, not only enhances deep understanding of the topological contribution to the physical properties of the material, but also improves the magnetic and electromagnetic properties of materials by modulating the topology of the materials. One of the interdisciplinary research fields between materials science and topology is analyzing the topological influence on spin texture and magnetic domain by observing spin states and (magnetic and ferroelectric) domains. Recently, topological spin texture, including vortex, skyrmion, meron and so on, in magnetic materials caused widespread attention in the academic community, especially skyrmion. Introduced by the British particle physicist Tony Skyrme, skyrmionis one type of particles related to baryons, including the superposition of baryons and resonant state. Skyrmion, which is a quasi-particle and a topological soliton, is the nontrivial and classical solution of nonlinear sigma mode. Researchers observed skyrmion in various fields, including classical liquid, liquid crystal, Bose-Einstein condense and quantum Hall magnet. Take quantum Hall magnet for example, when the filling factor n=1, exchange interaction between electrons will induce the full polarization of electron spin though Zeeman energy is zero, which makes all electrons occupy the lowest spilled Landau level and all of spins align along the direction of magnetic field. In a single-particle picture, the added electron will occupy the next spilled Landau level. However, two-dimensional system can arrange electrons to two energy levels to decrease exchange interaction by the formation of skyrmions, because the energy consumption to form skyrmion is about the half of exchange interaction energy to flip an electron spin. The spin configuration still carries one unite electron charge, but refers to more than one electron spin flip.

Vortex, skyrmion, meron and other states can be distinguished by topological invariant, as shown in the following figure:

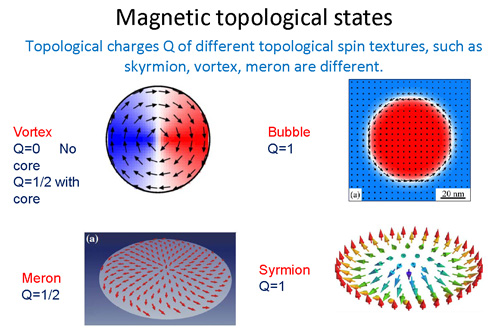
Skyrmion states have been theoretically predicted to exist in magnets with the Dzyaloshinsky-Moriya interaction (DMI). Recently, many experiments have proved their existence in helical magnets, such as MnSi and Fe_1−xCo_xSi. However, most of the skyrmions occurring in helimagnets were induced by an external magnetic field, only at low temperatures, which limits the application of Skyrmions in spintronics. Efforts have been made to resolve part of these problems.Skyrmions’ existing in helimagnets isalways associated with chiral magnetic interactions, the so-called DMI, which favours canted spin configuration and nontrivial spin textures, such as helimagnet or skyrmions. Despite all these efforts, neither spontaneous skyrmion-like magnetic ground states at or above room temperature have been reported, nor skyrmions are observed in magnets without DMI. The group headed by Prof. ZHANG Zhidong at Shenyang National Laboratory for Materials Science, Institute of Metal Research noted that the magnetostatic interaction favours spin canting and divergence-free spin alignment to reduce the total energy, an effect similar to that of the DMI. For example, confined magnetic thin films can exhibit variant topological spintextures such as vortex-like or meron-like states. They observed a spontaneous ground state of skyrmion-like configuration with the help of competition of exchange, magnetocrystalline anisotropy and demagnetization energies in Co/Ru/Co nanodisks without the DMI by micromagnetic simulations. The skyrmion state can be stable even in an external magnetic field of 0.44 T applied in +z direction. They observed anunusual dynamical behaviour of skyrmions in nanodisks. They found that the guiding center (Rx,Ry), defined by the moment of topological density of Skyrmions, displays a star-like trajectory in a pulsed magnetic field and a hexagonal trajectory after the field is switched off, which is different from the dynamics of vortices and bubbles. Moreover, the gyration of skyrmions in the bottom nanolayer without the presence of a field can be stimulated by the motion of skyrmions in the top nanolayer due to the strong coupling between skrymions in top and bottom nanolayers.Their study suggests a new approach to the generation of skyrmion textures in various confined systems but not limited to a magnetic one, reveals coupling effect between spin textures in magnetic nanodiscs, greatly enriches the dynamical behavior of topological structure and enhances deeply understanding of the influence of magnetic exchange coupling on topological density. The relevant research results was published at Phys. Rev. B88 (2013) 054403.

Fig. 1. (a) Sketch of a Co/Ru/Co nanodisk. (b)Micromagnetic simulation result for a Co (20 nm)/Ru (2 nm)/Co (20 nm) nanodisk. Arrows and colors correspond to the directions of the local magnetization and the magnitude of the out-of-plane magnetization component (Mz) at every point, respectively. Spin textures in both the top and the bottom nanolayers are skyrmions. (Image by IMR)

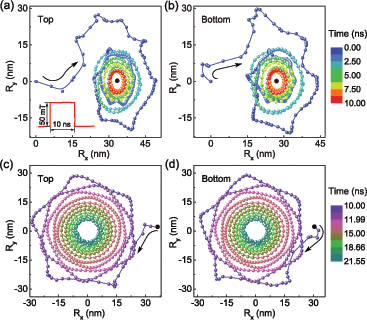
Fig. 2. (a, b) Trajectories of the guiding centers of skyrmions in both the top and the bottom nanolayers when a pulsed magnetic field is applied to the top nanolayer. (c, d) Gyrotropic motion of the guiding centers of skyrmions after the applied magnetic field is switched off. Colors are used to indicate time-dependent positions of (Rx, Ry). The filled black circle represents the new equilibrium position in the magnetic field. (Image by IMR)

Resonant excitations of confined systems have aroused much attention because of their potential application in future microwave devices and spintronics.Under resonant excitations, the motion of topological objects exhibits circular, elliptical or even stadium-like dynamics.However, more complex non-linear resonant excitations of topological objects in confined systems have seldom been reported and the associated physical mechanism also remains unclear. The research groupinvestigated the resonant excitations of coupled skyrmions in Co/Ru/Co nanodisks activated by a single-frequency microwave magnetic field and observed flower-like dynamics.The novel non-linear resonant excitations can be controlled systematically by the amplitude and frequency of the external magnetic field, such as from a circular trajectory to different flower-like ones.The flower-like dynamics of coupled skyrmions is always accompanied by an excitation of an eigenfrequency near 1.15 GHz, which is strongly associated with the large non-local deformation of the topological density distribution of coupled skyrmions. When the two types of resonant modes (clockwise and counterclockwise) were simultaneously stimulated, the flower-like trajectories were formed.These results distinguish a skyrmion from other topological objects in dynamics and will be instrumental to the manipulation of skyrmions forapplications. The relevant research results was published at Scientific Report 4 (2014) 6153.

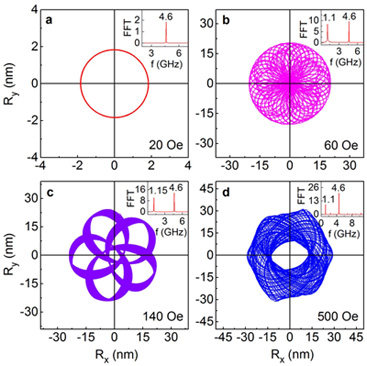
Fig. 3. Influence of the amplitude of a microwave field on the trajectory of the guiding center. The frequency of the microwave field is 4.60 GHz. (a), (b), (c) and (d) show the trajectories of the guiding center in 30 , 50 ns when the skyrmion is excited by a field of 20, 60, 140 and 500 Oe, respectively. The insets in the upper-right corners show the corresponding FFT spectra. (Image by IMR)

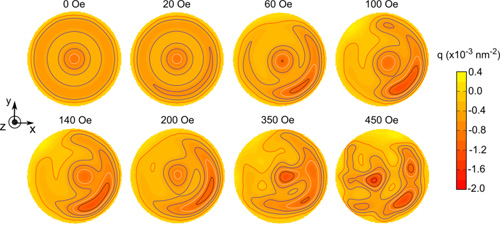
Fig. 4. The topological density distribution of skyrmion in different microwave fields. The frequency of the microwave field is 4.60 GHz and the amplitudes are in the range 0, 450 Oe. The figure shows the distribution at the time that D is maximal in one period. Tocompare the results easier, the distribution has been rotated by hand. The topological density distribution has radial symmetry without applied field and with increasing field amplitude, the deformation of the distribution increases and large non-local deformation takes place. (Image by IMR)