For fatigue damage evaluation and fatigue life prediction of materials, the classical Basquin equation (1910) and Coffin-Manson equation (1954) respectively choose the stress amplitude and plastic strain amplitude as factors to evaluate the fatigue damage. However, for different materials, the strain amplitude usually varies at the same stress amplitude, and so as the different stress amplitude at the same strain amplitude. In brief, it is nearly impossible to control both of the two amplitudes to the same values during the cyclic loading tests. This condition brings problems to the evaluation of fatigue properties: both of the factors are un-neutral and even injustice; conclusions often rely on the factor we choose. To this issue, after a long-term comprehensive study, the research group of Prof. ZHANG Zhefeng from the Materials Fatigue and Fracture Division, Shenyang National Laboratory for Materials Science (SYNL), Institute of Metal Research, Chinese Academy of Sciences (IMR, CAS) proposes the hysteretic energy-based fatigue damage model, which combines the stress and strain amplitudes by considering the hysteretic energy as the main damage factor.
1. Proposal of energy-based fatigue model. Fatigue fracture is a result of fatigue damage accumulation. In this model, fatigue damage is valued by the transition of hysteresis energy. For a single cycle, the damage accumulated effectively can be described as D=1/Nf=(Wa/W0)β, herein , the hysteresis energy(Wa) is decided by the external loading conditions, the fatigue toughness (W0) and damage transformation exponent (β) reflect the fatigue damage resistance ability of the materials. For the two internal factors, W0 possesses positive correlation with the static toughness U and represents the fatigue damage capacity of materials ; β is correlated with microscopic deformation mechanism, and represents the rate of fatigue damage accumulation. In this way, this energy-based model provides an objective method for fatigue damage evaluation and fatigue life prediction.
2. Applications of energy-based fatigue model. As a model with perspicuous physical image, this model is more applied than fatigue damage measurement and life prediction. Firstly, it ensures the justice of the evaluation of fatigue resistance. The value of hysteresis energy comprehensively reflects both the stress amplitude and the strain amplitudes, leading to a relatively objective evaluation. Secondly, the model can reveal the internal damage mechanisms through the parameters W0 and β. For instance, in Cu-Al alloys and Fe-Mn-C steels, W0 both increase linearly with the synchronous improvement of strength and ductility, while β displays opposite trends with the planarity of deformation mechanism in the two alloy systems. Further analysis on the deformation behaviors show that the contrary trends of could be owing to the different intrinsic mechanisms for deformation planarity. Thirdly, effective strategies for the improvement of fatigue resistance can be deduced according to the model. As fatigue damage can be considered as a process of energy accumulation, increasing the fatigue damage capacity (increase W0) and decreasing the fatigue damage accumulation rate (increase β) are thus the fundamental solutions for the improvement of fatigue properties. In addition, both the Basquin equation and the Coffin-Manson equation can be deduced from this energy model through reasonable simplification, which reflect its rationality and universality.
The above research results are published in Acta Materialia 83 (2015) 341 , Acta Materialia103 (2016) 781 and Scientific Reports 5 (2015) 9550.
This work is financially supported by the National Science Fund for Distinguished Young Scholars and National Natural Science Foundation of China.
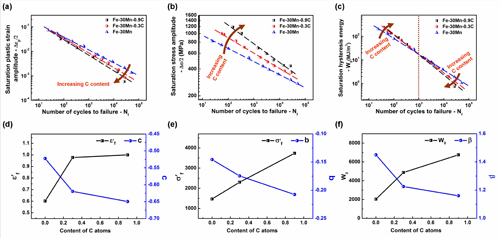
Fig1. Fatigue life curves of Fe-Mn-C steels. (a) Relationships between plastic strain amplitude and fatigue life (Coffin-Mansion equation). (b) Relationships between stress amplitude and fatigue life (Basquin equation). Opposite tendency of fatigue properties can be obtained through evaluations by strainand stress amplitudes.
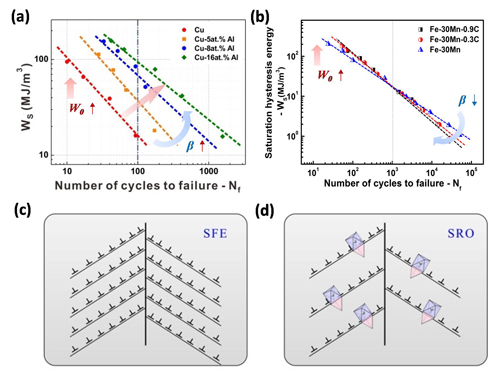
Fig2. Applications of energy-based fatigue model. (a)(b) Relationships between energy and fatigue life of (a) Cu-Al alloys and (b) Fe-Mn-C steels. (c)(d) Influences of SFE and SRO on microscopic deformation mechanisms in (c)Cu-Al alloys and (d) Fe-Mn-C steels.

Fig.3. Strategies for the improvement of fatigue properties: increasing the fatigue damage capacity and decreasing the fatigue damage accumulation rate.
Contact:
Prof. ZHANG Zhefeng
Email: zhfzhang@imr.ac.cn
Institute of Metal Research, Chinese Academy of Sciences, 72 Wenhua Road, Shenyang, Liaoning, 110016, China
Key Words:
Low-cycle Fatigue, Hysteresis Energy, Damage Mechanism, Fatigue Life Prediction