Two-phase materials are widely applied due to their beneficial combination of mechanical, physical, and electrical properties compared to their constituent elements. Therefore, it is significant for the design and development of materials to predict their properties based on constituent phase’s relevant properties.
How to predict the elastic properties of a composite such as Young’s modulus, shear modulus, and Poisson’s ratio have always attracted much attention. The previous researches only give different upper and lower bounds of the elastic moduli, yet the accurate values cannot be obtained.
Recently, a unified equation calculating the Young’s (shear) modulus of two-phase materials with discrete second phases was derived by Dr. ZHANG Zhenjun in Prof. ZHANG Zhefeng’s group in Institute of Metal Research, Chinese Academy of Sciences (IMR, CAS), based on the traditional parallel and series connection models and infinitesimal calculus, and it can be used to predict the mixed Young’s and shear moduli accurately. The equation is expressed as follows:
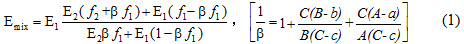
In (1), E1, f1 and E2, f2 are the elastic moduli and volume fractions of the matrix and second phase, respectively, and A, B, C, a, b and c are the axial lengths of each side of the equivalent unit, as illustrated by Fig. 1a. The parameter β reflects various sizes, shapes and distributions of the second phases, which has a value range of 0~1. β=0 reflects a parallel connection; β=1 reveals a series connection; β=1/2 represents a 2D square in square connection and β=1/3 indicates a 3D cube in cube connection, which corresponds to the case with equiaxed and homogeneously distributed second phases. The derivation process and the final expression of shear modulus G are completely analogous to those for E. For elastically isotropic composites, the Poisson′s ratio can be further calculated according to E and G.
Comparison with a plentitude of finite element simulations (Fig. 1b-1d) and numerous previous experimental investigations (Fig. 2) show a large consistency between the results and the analytic expressions derived, confirming the adequacy of the present approach. From Fig. 2, it can be seen that compared with the upper and lower bounds given by various previous models (dashed lines in Fig. 2), the present model ( red solid lines in Fig. 2) gives accurate predictions on the mixed Young’s modulus, shear modulus and Poisson′s ratio of various composites with different volume fraction of second phases.
From a theoretical point of view, the model utilizes the infinitesimal calculus in the calculation of mixed modulus for the first time, which not only gives the accurate calculation of mixed modulus, but also derives a unified expression for calculating the moduli of two-phase materials with discrete second phases with different sizes, shapes and distributions. From an applied point of view, the model has handy parameters and simple calculations, which largely simplifies the prediction process. Besides, if the above modulus E is replaced by the conductivity S, the present model can also be applied for predicting the mixed conductivity of two-phase materials because of the similarity between the electrical conductivity and elastic moduli.
This work has been recently published online in Physical Review B.

Figure 1 Schematic representation of the unit cell of two-phase composites (a) and FEM verification results (b-d): (b) and (c) are the results of 2D square in square connection and 3D cube in cube connection (including sphere second phases), respectively and (d) are the results for various β values. (Image by IMR)

Figure 2 Comparisons between several model predictions and the analytical expressions derived here with reported experimental results for elastic properties of two-phase composites: (a-g) Young’s modulus, (h) shear modulus and (i) Poisson′s ratio. It shows that the suggested model leads to more concise and accurate predictions than previous bounds. (Image by IMR)