Quasicrystals are a unique class of ordered solids that display long-range aperiodicity, which distinguishes them from ordinary crystals. The discovery of quasicrystals fundamentally alters how scientists in chemistry, physics and materials science conceive of solid matters. Extensive studies have provided explicit knowledge for understanding and modeling the atomic arrangements in intermetallic quasicrystals. However, understanding the atomic origin and growth of quasicrystals is still challenging, since they cannot grow like crystals, where the nucleus surface acts as a template for copying a unit cell via local interactions.
Dislocations in crystals naturally break the symmetry of the bulk, introducing local atomic configurations with symmetries such as five-fold rings. And interestingly, icosahedral clusters consisting of a small amount of atoms which show five-fold rotations have low free energy, and can exist in liquid metals. And quasicrystals can form based on icosahedral clusters present in undercooled liquid during solidification. It is also known that five-fold rings of atoms may be produced at dislocation cores in crystals. This knowledge about quasicrystals and dislocations implies that dislocations in crystals might serve as nucleation sites for icosahedral clusters.
Recently, Dr. YANG Zhiqing and Prof. YE Hengqiang from Institute of Metal Research, Chinese Academy of Sciences studied precipitation in strained Mg-Zn alloys using atomic resolution electron microscopy techniques. It was demonstrated that the formation of extended binary quasicrystalline precipitates with Penrose-like random-tiling structures began with chemical ordering within the pentagonal structure at cores of prismatic dislocations in Mg-Zn alloys. Atomic resolution observations indicate that icosahedral chains centred along [0001] pillars of Zn interstitial atoms are formed templated by the five-fold rings at dislocation cores. They subsequently form columns of rhombic and elongated hexagonal tiles parallel to the dislocation lines. Quasicrystalline precipitates are formed by random tiling of these rhombic and hexagonal tiles. Such precipitation may impact on dislocation glide and hence the strength of alloys.
This work entitled “Precipitation of binary quasicrystals along dislocations” has been published online in Nature Communications.

Figure 1. Zn segregation at a dislocation core and precipitation of binary quasicrystals. a HAADF-STEM image showing Zn segregation at a dislocation core. b, c Enlarged images of the dislocation core region shown in (a). The intensity profile at the bottom of (b) indicates that the amount of octahedral Zn atoms is twice that of the middle column. Laves MgZn2 icosahedra are superimposed on (c). Those atomic columns indicated by arrows are still mostly occupied by anti-site Zn or Mg atoms, and the two columns circled in dots are not yet occupied. d, e Lattice strain around the dislocation measured, indicating presence of a dislocation nearby the upper left icosahedral chain shown in (b). f Atomic structure of typical precipitate in samples annealed at 613 K for 60 min. The inset is a FFT pattern of the image, showing ten reflections distributing on a ring, as indicated by arrows. g, h Enlarged images showing local five-fold rotation of rhombic tiles and elongated hexagonal tiles, respectively. (Image by IMR)
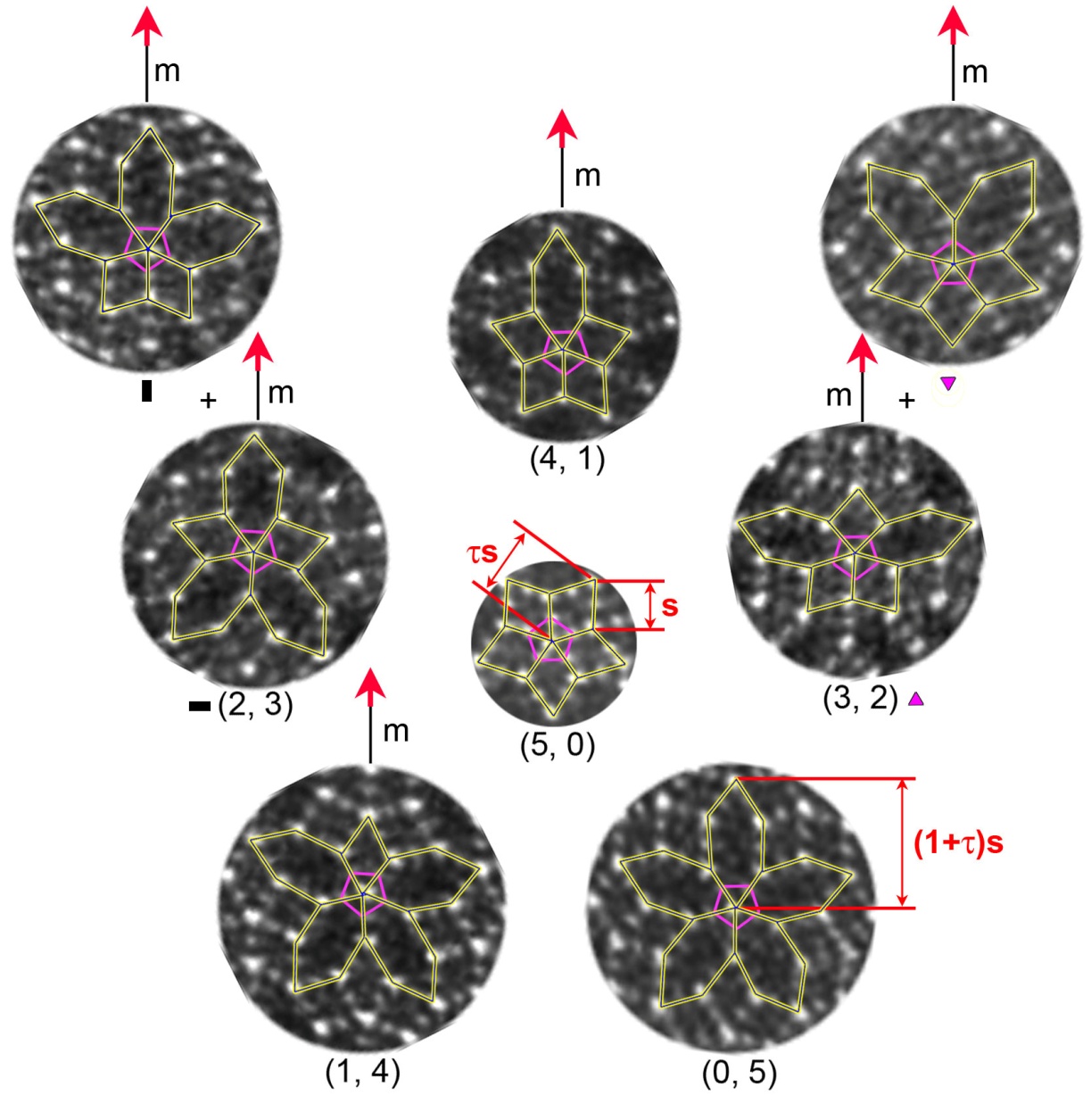
Figure 2. Chemically ordered icosahedral chains and surrounding rhombic or elongated hexagonal tiles. One chemically ordered icosahedral chain (as indicated by the purple pentagon in each case) can be shared by n (n = 5, 4, 3, 2, 1, or 0) rhombic tiles and 5-n elongated tiles, which is indicated by (n, 5-n). There are two different arrangements of rhombic and elongated hexagonal tiles for cases of (3, 2) and (2, 3), as indicated by differently orientated purple triangles and black rectangles, respectively; while there is only one for others. There is ‘one’ mirror plane for structures of (1, 4), (2, 3), (3, 2) and (4, 1), while structures (5, 0) and (0, 5) have ‘five’ mirror planes. And a specific orientation of these local structures is indicated by a red arrow. The edge length of rhombic and elongated hexagonal tiles is s (s = 0.45 nm), and their longer diagonals are ts and (1+t)s. is the golden mean. The distortion of rhombic and elongated hexagonal tiles is mainly from sample drift during imaging. (Image by IMR)