The Ising model has been well – known to be a simple model providing profound physical significances, which is helpful for discovering principles in our physical world. It has been not only conceived as a description of magnetism in crystalline materials, but also applied to various phenomena as diverse as the order-disorder transformation in alloys, the transition of liquid helium to its superfluid state, the freezing and evaporation of liquids, the behavior of glassy substances, and even the folding of protein molecules into their biologically active forms. In accordance with the Yang and Lee’s theorems, the problem of an Ising model in a magnetic field is mathematically equivalent to a lattice gas. The widespread interest focusing on the Ising model is primarily derived from the fact that it is one of the simplest examples describing a system of interacting particles (or atoms or spins). The Ising model forms an excellent test case for any new approximation method of investigating systems of interacting particles, specially, of understanding the cooperative phenomena and the critical behaviors at/near the critical point of a continuous phase transition. Furthermore, the 3D Ising model can serve as a testing model for the evolution of a system of interacting particles (or spins) from infinite temperature down to zero, as one could see the analogy of temperature in the thermodynamics to a variable of time in the dynamics. Therefore, the exact solutions obtained are quite helpful for understanding the evolution of an equilibrium infinite system not only for a magnet, but also even for our Universe. In addition, the formal theory of equilibrium phase transitions has found applications in problems such as continuous quantum phase transitions, constructing field and string theories of elementary particles, the transition to chaos in dynamical systems, the long – time behavior of systems out of equilibrium and dynamic critical phenomena.
In a previous work (published in Philosophical Magazine 87 (2007) 5309), Prof. ZHANG Zhidong of Institute of Metal Research (IMR), Chinese Academy of Sciences, reported the conjectures on the 3D Ising model on simple orthorhombic lattices, together with details of calculations for a putative exact solution. Two conjectures, an additional rotation in the fourth curled-up dimension and the weight factors on the eigenvectors, were proposed to serve as a boundary condition to deal with the topologic problem of the 3D Ising model.
In a recent work (published in Advances in Applied Clifford Algebras 29 (2019) 12), Prof. ZHANG Zhidong of IMR, Prof. Osamu Suzuki of Nihon University, Japan and Prof. Norman H. March of Oxford University, England developed a Clifford algebra approach for 3D Ising model. By utilizing some mathematical facts of the direct product of matrices and their trace, the researchers expand the dimension of the transfer matrices of the 3D Ising system by adding unit matrices (with compensation of a factor) and adjusting their sequence, which do not change the trace of the transfer matrices (Theorem I: Trace Invariance Theorem). The transfer matrices are re-written in terms of the direct product of sub-transfer-matrices, where each sub-transfer-matrix stands for the contribution of a plane of the 3D Ising lattice and interactions with its neighboring plane. The sub-transfer-matrices are isolated by a large number of the unit matrices, which allows us to perform a linearization process (Theorem II: Linearization Theorem). It is found that locally for each site, the internal factor in the transfer matrices can be treated as a boundary factor, which can be dealt with by a procedure similar to the Onsager-Kaufman approach for the boundary factor in the 2D Ising model. This linearization process splits each sub-transfer matrix into 2n sub-spaces (and the whole system into 2nl sub-spaces). Furthermore, a local transformation is employed on each of the sub-transfer matrices (Theorem III: Local Transformation Theorem). The local transformation trivializes the non-trivial topological structure, while it generalizes the topological phases on the eigenvectors. This is induced by a gauge transformation in the Ising gauge lattice that is dual to the original 3D Ising model. The non-commutation of operators during the processes of linearization and local transformation can be dealt with to be commutative in the framework of the Jordan-von Neumann-Wigner procedure, in which the multiplication in Jordan algebras is applied instead of the usual matrix multiplication (Theorem IV: Commutation Theorem). This can be realized by time-averaging t systems of the 3D Ising models with time evaluation. This work provides a mathematical base for the Zhang’s two conjectures. The four Theorems proved in this work develop an approach for a topological quantum statistical mechanics, in which the contributions of non-trivial topological structures are dealt with, a time average is considered and the Jordan algebras is utilized in the framework of the Jordan-von Neumann-Wigner procedure. Furthermore, this work discovers a novel topological phase in the 3D many-body interacting systems. The advance in the exact solution of the 3D Ising model is helpful for understanding the interactions between matters, the contributions of topology to physical properties, the nature of space, the spontaneous emergence of time and so on. It can find its place for developments and applications in condensed matter physics, statistics mechanics, high-energy physics, biology and computer sciences.
Links to papers for exact solution of 3D Ising model:
1. Z.D. Zhang, Philosophical Magazine 87 (2007) 5309. https://doi.org/10.1080/14786430701646325
2. Z.D. Zhang, Chinese Physics B 22 (2013) 030513. https://doi.org/10.1088/1674-1056/22/3/030513
3. Z.D. Zhang, O. Suzuki and N.H. March, Advances in Applied Clifford Algebras 29 (2019) 12. https://doi.org/10.1007/s00006-018-0923-2
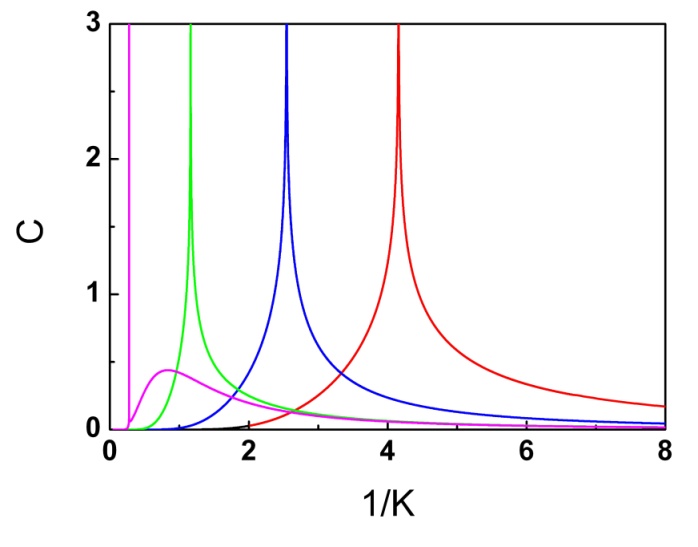
Temperature dependence of the specific heat C for the 3D simple orthorhombic Ising lattices with K’ = K’’ = K, 0.5 K, 0.1 K and 0.0001 K (from right to left). (Image by IMR)